Guía de Trabajos Prácticos

Cátedra: Termodinámica

Trabajo Práctico: Equilibrio Físico de Sustancias Puras - Medición de Presión de Vapor

Carrera: Ingeniería Química

Objetivos

Analizar el equilibrio entre fases para una sustancia pura.

Introducción

Cuando un líquido está en equilibrio con su vapor a una temperatura dada, el vapor ejerce una presión que sólo depende de la temperatura, y que se denomina “presión de vapor”.

El valor de la presión de vapor es independiente de las cantidades de líquido y vapor presentes, por lo cual, a distintas temperaturas se obtendrán distintos valores de presión de vapor, los cuales constituirán puntos de la “curva de saturación” para la sustancia en estudio.

Fundamentos

El efecto de la temperatura sobre la presión de vapor puede analizarse termodinámicamente a partir de la expresión de la condición general de equilibrio:

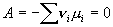
Para un compuesto puro: ;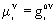

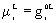
Luego: 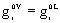. Diferenciando: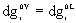

g es una función de estado de T y P \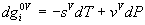

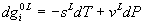
de donde se puede concluir que:

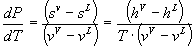(I)

Esta es la ecuación de Clapeyron, que es rigurosa y también aplicable a los equilibrios S-L y S-V.

Al ser una expresión rigurosa, puede ser utilizada como test de consistencia termodinámica.

A partir de (I) y considerando como hipótesis válidas que:

. v^L << v^V (esto ocurre lejos del punto crítico)

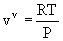. (ecuación de estado de los gases ideales)

se arriba a: 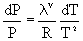(II)

Esta es la ecuación de Clausius-Clapeyron, la que brinda una relación funcional fácilmente integrable entre la temperatura y la presión de saturación para el equilibrio Líquido-Vapor (con similares consideraciones es aplicable al equilibrio Sólido-Vapor).

Las ecuaciones de Clapeyron y de Clausius-Clapeyron son herramientas que permiten evaluar en forma crítica los resultados de las mediciones de temperaturas y presiones de saturación, efectuar correlaciones semiempíricas, estimar propiedades, etc.

Técnica experimental para la construcción de una curva de saturación

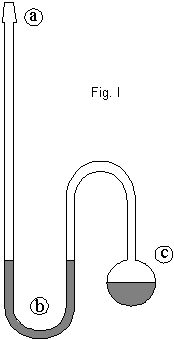
En el dispositivo de la Fig. I, llamado ISOTENISCOPIO, se coloca en (c) la sustancia cuya presión de vapor se desea medir. Para eliminar el aire del sistema, que introduciría errores, se hace vacío en el isoteniscopio y en las otras ramas, incluido el manómetro (8), Fig. II.

Luego se inclina el equipo y se hace pasar líquido desde (c) hasta (b), de modo de formar un sello de líquido en (b) de aproximadamente 3 cm.; posteriormente se sumerge el isoteniscopio en el baño termostatizado (12), con lo que ambas ramas en el tubo (b) se desequilibran. Para equilibrar ambos niveles se puede hacer ingresar aire seco por (10) o bien hacer vacío nuevamente.

Una vez logrado esto, se realizan las mediciones de presión de vapor ya que, equilibrando ambas ramas del tubo (b) se asegura que la presión dentro de (c) sea la misma que se mide en el manómetro de Hg (8).

Aunque se haya hecho entrar aire a la izquierda del sello (b), debe cuidarse muy especialmente que el aire no ingrese en (c); esto es lo que asegura que el manómetro mida la presión de vapor de la sustancia pura.

La temperatura se mide con un termómetro (7), y puede variarse mediante el uso de un baño termostatizado.

Esquema del dispositivo utilizado

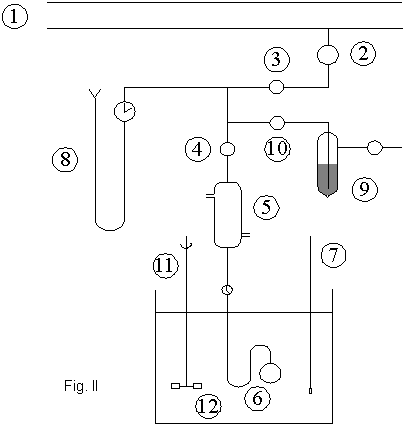
(1) Distribuidor de vacío central (5) Condensador (9) Desecador de aire

(2) Válvula, conecta a vacío central (6) Isoteniscopio (10) Válvula ingreso de aire

(3) Válvula (7) Termómetro (11) Agitador

(4) Válvula (8) Manómetro de Hg (12) Baño termostatizado

Tratamiento de datos

Se construye la curva de saturación para el equilibrio L-V (P vs T_sat), sobre la que pueden descartarse los puntos erráticos o dudosos.

Luego se utilizará la ecuación (II), que ofrece distintas alternativas de integración, de acuerdo a la variación de l^v con la temperatura, según:

1) l^v = cte ¹ f (T)

Recordando la expresión (II):

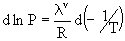
e integrando esta expresión entre T_o y T (cuyas presiones de vapor son, respectivamente, P_o y P), se tiene que:

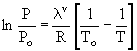(III)

La ecuación (III) tiene la forma

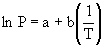(IV)

1.a) Con los datos experimentales P vs. T_sat puede construirse la curva ln P vs. 1/T.

1.b) Mediante el método de los cuadrados mínimos puede obtenerse los coeficientes a y b de la expresión (IV) y verificar la utilidad de la misma para interpolar valores de P y T de saturación.

1.c) Estimar valores de l^v entre un par de valores de P y T de saturación

2) l^v = f (T)

Para gases perfectos y líquidos incompresibles puede demostrarse que

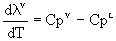; luego

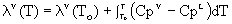(V)

De aquí pueden presentarse distintas alternativas de integración:

2.a) Cp^v – Cp^L = cte Þ l^v(T) = l^v(T_o) + (Cp^v – Cp^L)(T-T_o) ;

que es de la forma l^v(T) = a’ + b’T

Reemplazando en (II) se tendrá una función del tipo:

ln P = A + B (1/T) + C ln T (VI)

A partir de los datos experimentales pueden obtenerse los coeficientes A, B y C de la expresión (VI) y verificar la utilidad de dicha expresión para interpolar valores de P y T de saturación.

2.b) (Cp^v – Cp^L) = a” +b”T

Reemplazando en (V), integrando y luego reemplazando l^v = f (T) en (II), se arriba a una expresión del tipo:

ln P = A’ + B’ (1/T) + C’ ln T + D’T (VII)

Se deja para demostrar a qué son iguales los coeficientes a, b, A, B, C, A’, B’, C’ y D’ en los distintos casos.

Para completar el análisis de los datos experimentales se pueden comparar éstos, así como los valores que proveen las ecuaciones (IV), (VI) y (VII), con los datos que provee la bibliografía para la sustancia utilizada.

Cuestionario

a) De la expresión de equilibrio entre fases para una sustancia pura, desarrollar la ecuación de Clausius-Clapeyron.

b) Suponiendo que l^v es función de la temperatura, obtener las expresiones de las constantes de las ecuaciones (VI) y (VII).

c) Enumerar las posibles causas de error.